二叉树 游戏数据结构

灵枫

二叉树定义
一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根结点和两棵分别称为左子树和右子树的、互不相交的二叉树组成。


结构特点
每个结点最多只有两个孩子结点，即结点的度不大于2 ,子树有左右之别，子树的次序（位置）不能颠倒。


二叉树的性质

二叉树具有以下重要性质：

性质1 二叉树第i层上的结点数目最多为2i-1(i≥1)。

证明：用数学归纳法证明：
　 归纳基础：i=1时，有2i-1=20=1。因为第1层上只有一个根结点，所以命题成立。
　归纳假设：假设对所有的j(1≤j 　归纳步骤：根据归纳假设，第i-1层上至多有2i-2个结点。由于二叉树的每个结点至多有两个孩子，故第i层上的结点数至多是第i-1层上的最大结点数的2倍。即j=i时，该层上至多有2×2i-2=2i-1个结点，故命题成立。


性质2 深度为k的二叉树至多有2k-1个结点(k≥1)。

证明:因为深度为k的二叉树,其结点总数的最大值是将二叉树每层上结点的最大值相加,所以深度为k的二叉树的结点总数至多为
故结论成立.


性质3 在任意-棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1。

证明：
若设度为1的结点有 n1 个，结点总数为 n，分支总
数为 B，则根据二叉树的定义，
n = n0 + n1 + n2 B = 2n2 + n1 = n - 1
因此，有 2n2 + n1 = n0 + n1 + n2 - 1
n2 = n0 - 1 n0 = n2 + 1

满二叉树和完全二叉树是二叉树的两种特殊情形。
1、满二叉树(FullBinaryTree)
　一棵深度为k且有2k-1个结点的二又树称为满二叉树。
　满二叉树的特点：
　　（1） 每一层上的结点数都达到最大值。即对给定的高度，它是具有最多结点数的二叉树。
　　（2） 满二叉树中不存在度数为1的结点，每个分支结点均有两棵高度相同的子树，且树叶都在最下一层上。

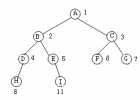
(a) 一棵满二叉树




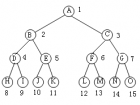
(b) 一棵非满二叉树


一棵深度为k，有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时，则这棵二叉树称为完全二叉树。完全二叉树的特点是：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。

显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树。

如图5-4（a）所示为一棵完全二叉树，图5-4（b）为一棵非完全二叉树。


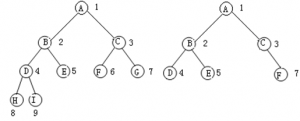
(a) 一棵完全二叉树    (b) 一棵非完全二叉树



性质4
具有 n (n >= 0) 个结点的完全二叉树的高度为
log2(n + 1)向上取整 或 log2 n 向下取整 + 1

性质5 如果将一棵有n个结点的完全二叉树自顶向下，同一层自左向右连续给结点编号, 1, 2,…,n，且使该编号对应于数组的下标，则有以下关系：
若i = 1, 则 i 是根结点，无父结点
若i > 1, 则 i 的父结点为 i/2 向下取整
若 2*i <= n, 则 i 有左儿子且为 2*i；否则，i 无左儿子。
若2*i+1 <= n, 则 i 有右儿子且为2*i+1；否则，i 无右儿子。
若 i 为偶数, 且 i < n , 则有右兄弟，且为 i + 1。
若 i 为奇数, 且 i <= n && i != 1, 则其左兄弟，且为 i-1